IT/모바일
✅ Big O 표기법
알고리즘의 효율에서 가장 중요한 부분은 ‘n이 커질 때 알고리즘의 단계가 얼마만큼 증가하는가’이고, 이것을 잘 나타내는 빅 O 표기법을 사용합니다. ►[알고리즘 + 자료구조 = 프로그램] 최선의 알고리즘을 찾는 기준
빅 O 표기법은 점근 표기법(Asymptotic Notation) 중 하나인데, 점근 표기법이란 ‘점근(漸近): 차츰 점, 가까울 근’이라는 이름에서 알 수 있듯이 알고리즘의 수행 시간을 대략적으로 나타내는 방법을 말합니다. 여기서 말한 ‘대략적으로’는 ‘정확하게’의 반대말이 아니라 ‘자세하게’의 반대말입니다.
소규모 데이터를 다루는 경우 우수한 성능의 알고리즘과 그렇지 않은 알고리즘 사이에 차이가 거의 없습니다. 퀵 정렬이 훨씬 우수한 성능을 갖고 있지만, 오히려 소규모 데이터를 정렬할 때에는 삽입 정렬을 사용하는 편이 더 나은 효율을 보이죠. 알고리즘 성능 차이는 대규모 데이터를 다룰 때 두드러집니다. 그 규모가 무한대에 가까워진다면 그 차이는 아주 분명해지겠죠.
대표적으로 사용하는 점근 표기법은 다음 3가지입니다.
- O(Big O) 표기법: 알고리즘 성능이 최악인 경우(수행 시간의 상한)를 나타낼 때 사용
- Ω(Big Omega) 표기법: 알고리즘의 성능이 최선인 경우(수행 시간의 하한)를 나타낼 때 사용
- Θ(Big Theta) 표기법: 알고리즘이 처리해야 하는 수행 시간의 상한과 하한을 동시에 나타냄
빅 O 표기법은 최악의 경우 알고리즘 수행 시간을 나타냅니다. 다시 말해 알고리즘을 사용하는 어떤 경우에도 보장되는 알고리즘의 성능이라고 할 수 있습니다. 최악의 경우에 대한 알고리즘 수행 시간이 가장 쓸모가 많다 보니 가장 많이 사용하는 알고리즘 성능 표기법으로 빅 O 표기법이 꼽히곤 합니다.
빅 O 표기법을 사용하는 방법은 대문자 O를 쓰고 그 옆에 괄호를 열고 닫은 후 그 안에 증가 함수를 넣습니다. 증가 함수는 입력 데이터의 크기 n에 대해 알고리즘의 수행 시간이 늘어나는 비율을 나타내는 함수입니다. 다음은 빅 O 표기법에서 가장 널리 사용되는 규모 함수들을 최선(가장 효율적)에서 최악(가장 비효율적)의 순서로 나열한 것입니다.

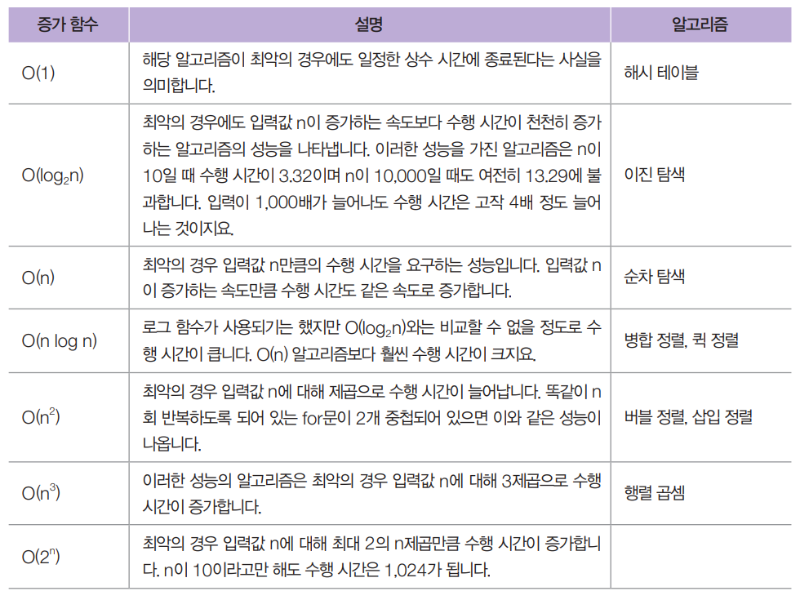
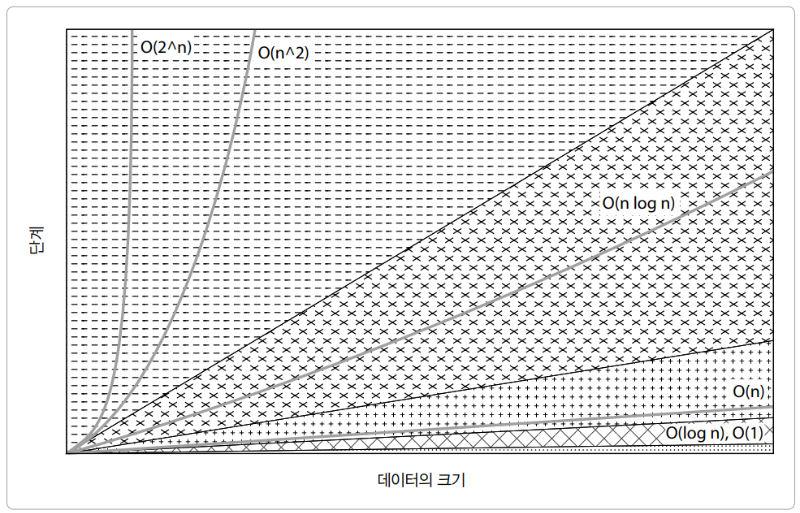
✅상수 시간
가장 효율적인 규모는 상수 시간 복잡도(Constant Time Complexity)입니다. 어떤 알고리즘이 n의 크기에 관계없이 동일한 단계만 필요한 경우 ‘알고리즘이 상수 시간으로 실행된다’고 말합니다. 상수 시간 알고리즘을 빅 O 표기법으로 표기하면 O(1)과 같습니다.
예를 들어 여러분이 온라인 서점을 운영하면서 매일 첫 번째로 방문하는 고객에게 무료로 책을 선물한다고 합시다. 이 고객을 customers 리스트에 저장한다고 하면 알고리즘은 대략 다음과 같은 형태입니다.

이 알고리즘의 단계를 나타내는 수식 T(n)은 다음과 같습니다.

고객이 아무리 많아도 이 알고리즘에는 하나의 단계만 필요합니다. 고객이 1,000명, 10,000명이더라도 한 단계로 끝나고, 조단위라 하더라도 한 단계면 충분합니다. 고객의 수를 x 축, 알고리즘의 단계를 y 축으로 하는 상수 시간 복잡도를 그래프로 그리면 [그림 1-1]과 같이 평평한 형태가 됩니다.
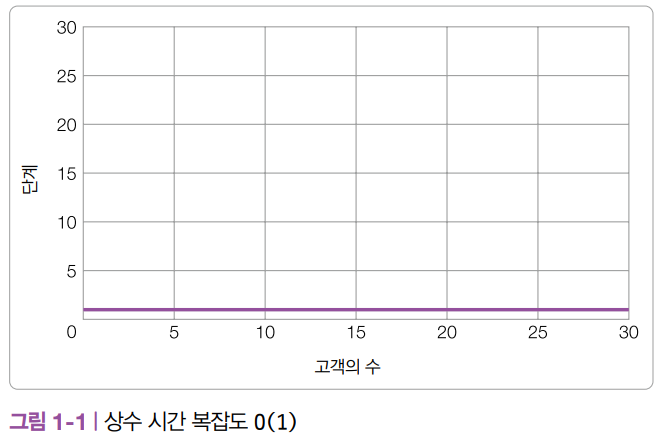
상수 시간 알고리즘은 [그림 1-1]과 같이 알고리즘이 완료될 때까지 필요한 단계가 일정합니다. 데이터 세트가 아무리 커지더라도 알고리즘의 실행 시간이 변하지 않으므로 가장 효율적인 알고리즘이라고 할 수 있습니다.
✅로그 시간
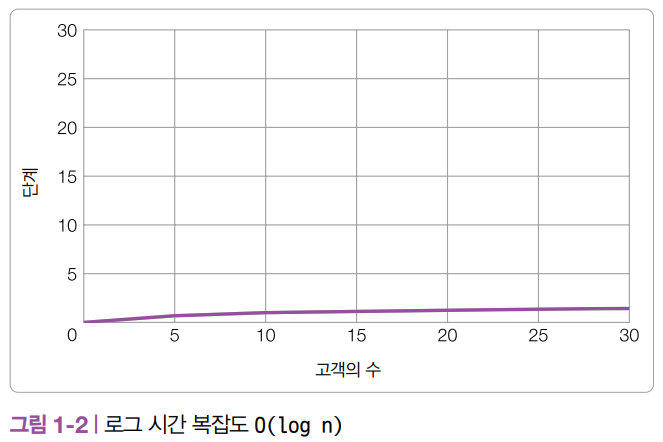
로그 시간 복잡도(Logarithmic Time Complexity)는 상수 시간에 이어 두 번째로 효율적인 시간 복잡도입니다. 데이터의 로그에 비례해 알고리즘의 단계가 늘어날 때, 알고리즘이 로그 시간으로 실행된다고 말합니다. 로그 시간 복잡도는 실행을 반복할 때마다 알고리즘의 탐색 범위를 1/2로 줄여 나가는 이진 탐색과 같은 알고리즘에서 볼 수 있습니다. 빅 O 표기법에서는 로그 시간 알고리즘을 O(log n)으로 표기합니다.
로그 시간 복잡도의 그래프는 [그림 1-2]와 같은 형태로 그릴 수 있습니다. 즉, 로그 시간 알고리즘은 데이터 세트가 커짐에 따라 알고리즘의 실행에 필요한 단계가 천천히 늘어나는 알고리즘을 말합니다.
✅선형 시간
로그 시간 복잡도 다음으로 효율적인 것은 선형 시간 복잡도(Linear Time Complexity)입니다. 선형 시간으로 실행되는 알고리즘은 데이터의 크기가 커지는 만큼 같은 비율로 단계가 늘어나는 알고리즘을 말하며, 빅 O 표기법에서는 O(n)으로 표기합니다.
매일 첫 번째로 방문하는 고객에게 무료로 책을 선물하는 대신, 고객 리스트를 훑어 보면서 이름이 B로 시작하는 고객에게 책을 선물한다고 가정해 보겠습니다. 고객 리스트가 알파벳 순으로 정렬되어 있지 않다면 다음 코드처럼 B로 시작하는 이름을 하나씩 탐색하며 찾아야 합니다.

고객이 다섯 명이라면 프로그램도 이름을 탐색하는 다섯 번의 단계를 거쳐야 합니다. 고객이 10명이면 10번, 20명이면 20번의 탐색 단계가 필요합니다. 따라서 이 프로그램의 시간 복잡도는 각각 free_book과 customers에 할당하는 단계와 고객 리스트에서 B로 시작하는 이름을 탐색하는 n번의 단계를 더해 다음과 같이 나타낼 수 있습니다.

빅 O 표기법에서는 상수 부분을 무시하고 f(n)을 지배하는 부분만 선택해 다음과 같이 나타냅니다.

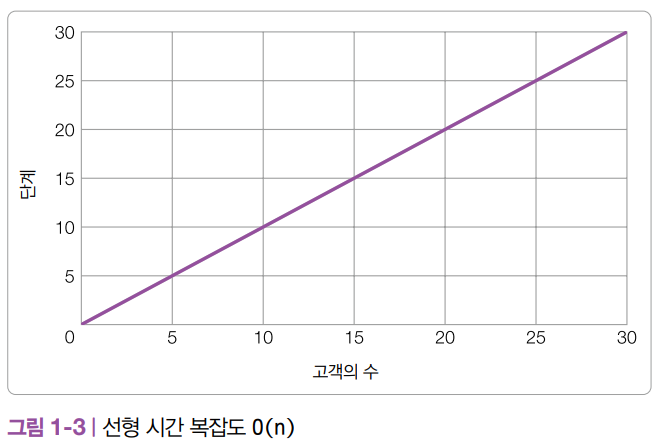
선형 시간 복잡도의 그래프는 [그림 1-3]과 같이 데이터 세트가 커지는 만큼 알고리즘의 실행에 필요한 단계도 같은 비율로 늘어납니다.
✅선형 로그 시간
선형 로그 시간(Log-Linear Time)을 따르는 알고리즘의 복잡도는 로그 시간 복잡도와 선형 시간 복잡도를 곱한 만큼 커집니다. 로그 시간으로 실행되는 알고리즘 O(log n)을 n번 반복하는 형태를 말하며, O(n log n)으로 표기합니다.
선형 로그 시간 알고리즘은 보통 데이터 세트를 작은 부분으로 나누고, 이들을 독립적으로 처리하는 형태를 취합니다. 병합 정렬과 같은 효율적인 정렬 알고리즘은 대부분 선형 로그 시간 복잡도를 따릅니다.
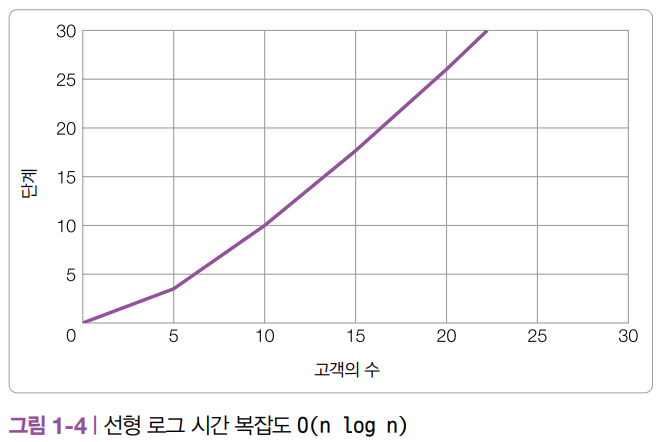
[그림 1-4]는 선형 로그 시간 복잡도를 그래프로 그린 모습입니다. 그래프에서 알 수 있듯, 선형 로그 시간 복잡도는 선형 시간 복잡도보다는 비효율적이지만, 2차 시간 복잡도보다는 효율적입니다.
✅2차 시간
2차 시간 복잡도(Quadratic Time Complexity)는 선형 로그 시간 복잡도 다음으로 효율적인 시간 복잡도입니다. 2차 시간으로 실행되는 알고리즘의 복잡도는 n의 제곱에 정비례하며, O(n**2)으로 표기합니다.
다음은 2차 시간 복잡도를 따르는 알고리즘의 예제입니다.

이 알고리즘은 숫자 리스트 numbers에 들어 있는 모든 숫자를 서로 곱해 변수에 저장한 후 출력합니다. 여기서 n은 numbers 리스트의 크기이므로, 이 알고리즘의 시간 복잡도 f(n)은 다음과 같이 나타낼 수 있습니다.

이 식의 (1 + 1) 부분은 각각 (i * j)를 변수 x에 저장하는 단계와 print 함수에 해당합니다. 두 번 중첩된 for 루프를 통해 곱셈과 출력을 n * n 번 반복합니다. f(n)은 다음과 같이 단순화할 수 있습니다.

한 번 더 단순화하면 다음과 같습니다.

마찬가지로 f(n)의 크기를 지배하는 부분이 n**2이므로 빅 O 표기법으로는 다음과 같이 나타낼 수 있습니다.

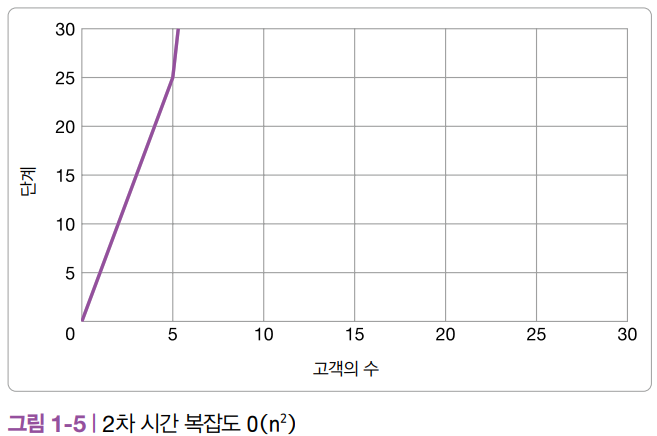
2차 시간 복잡도를 그래프로 그려보면 다음과 같습니다. 알고리즘에 1부터 n까지 또는 0부터 n−1까지 실행하는 루프가 두 번 중첩되어 있다면 그 알고리즘의 시간 복잡도는 최소한 O(n**2) 이상이겠죠. n의 제곱에 비례해 실행 시간이 늘어나는 삽입 정렬이나 버블 정렬과 같은 정렬 알고리즘의 상당수가 2차 시간 복잡도를 따릅니다.
✅3차 시간
3차 시간(Cubic Time)으로 실행되는 알고리즘의 시간 복잡도는 n의 세제곱에 정비례하며, O(n**3)으로 표기합니다. 다음은 3차 시간 복잡도를 따르는 알고리즘의 예제입니다.

이 알고리즘의 f(n)은 다음과 같습니다.

다음과 같이 단순화할 수도 있습니다.

2차 시간 복잡도와 마찬가지로 f(n)에서 가장 중요한 부분은 n**3입니다. n**3은 급격하게 커지기 때문에 만약 f(n)의 나머지 부분에 n**2이 포함되어 있더라도 무시할 수 있을 정도입니다. 따라서 빅 O 표기법에서는 다음과 같이 표현할 수 있습니다.

알고리즘에 0부터 n까지 실행하는 루프가 세 번 중첩되어 있다면 그 알고리즘은 3차 시간 복잡도를 따릅니다. 데이터 과학이나 통계와 관련된 일을 한다면 3차 시간 복잡도 문제를 자주 접하게 됩니다.
2차와 3차 시간 복잡도는 모두 다항 시간 복잡도에 속합니다. 다항 시간 복잡도(Polynomial Time Complexity)를 따르는 알고리즘은 O(n**a)에 비례하여 커지는데, 2차 시간은 a가 2인 경우, 3차 시간은 a가 3인 경우에 해당하겠죠. 알고리즘을 설계할 때는 가급적 다항 시간 알고리즘을 피하는 편이 좋습니다. 이런 알고리즘은 n이 커짐에 따라 알고리즘의 실행 시간이 급격하게 늘어날 수 있기 때문입니다. 하지만 가끔 피치 못하게 다항 시간 알고리즘을 사용해야 하는 경우에는 다음에 살펴볼 최악의 알고리즘과 비교했을 때 그나마 다항 시간 복잡도가 괜찮은 편이라고 생각하는 것이 위안이 될 거예요.
✅지수 시간
최악의 시간 복잡도로 꼽히는 것은 지수 시간 복잡도(Exponential Time Complexity)입니다. 지수 시간으로 실행되는 알고리즘의 복잡도는 데이터 크기의 지수식으로 표현됩니다. 어떤 상수 c를 n 제곱한 만큼 실행 단계가 커지는 알고리즘으로, 빅 O 표기법에서는 O(c**n)으로 표기합니다. 여기서 상수 c가 얼마나 큰지는 중요하지 않습니다. 문제는 지수인 n입니다.
다행히 지수 시간 복잡도가 자주 마주치는 문제는 아닙니다. 예를 들어, n개의 숫자로 이루어진 비밀번호를 가능한 모든 조합을 시도해 알아내려고 하는 경우 지수 시간 복잡도에 해당하며, O(10**n)으로 표기합니다. 다음 예제를 봅시다.

이 알고리즘을 완료하기 위해 필요한 단계는 n이 커짐에 따라 믿을 수 없을 정도로 빠르게 커집니다. n이 1이면 10번의 단계를 거쳐야 하고 n이 2이면 100번, n이 3이면 1,000번의 단계가 필요합니다. 언뜻 보기에는 지수 시간 알고리즘이 그렇게까지 빨리 커지는 것처럼 보이지 않지만 감당할 수 없이 커지는 건 순식간입니다.
여덟 자리의 비밀번호를 알아내려면 1억 번을 시도해야 하고, 열 자리의 비밀번호를 알아내려면 100억 번을 시도해야 합니다. 이제 비밀번호의 자릿수가 왜 그렇게 중요한지 깨달으셨죠? 만약 네 자리의 비밀번호를 사용한다면 이런 프로그램을 통해 손쉽게 비밀번호를 알아낼 수 있습니다. 반면 스무 자리의 비밀번호를 사용한다면 아마 해커가 죽을 때까지도 프로그램이 끝나지 않기 때문에 절대 알아낼 수 없습니다.
이런 식으로 비밀번호를 알아내는 것을 무차별 대입 알고리즘(Brute-Force Algorithm)이라고 합니다. 무차별 대입 알고리즘은 가능한 경우의 수를 전부 대입해 보는 알고리즘입니다. 보통 이 알고리즘은 비효율적이므로 최후의 수단으로만 사용해야 합니다.
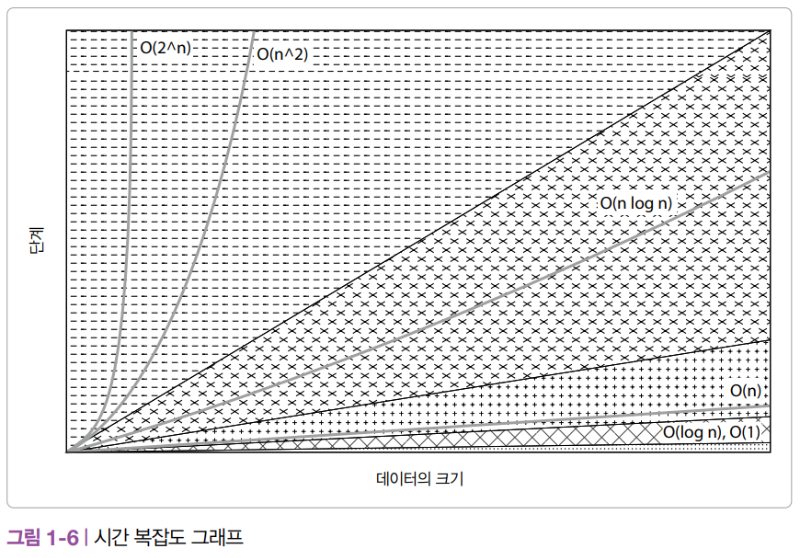
지금까지 설명한 알고리즘의 효율성은 다음과 같습니다.
✅최선과 최악
알고리즘의 실행 시간, 즉 성능은 데이터의 종류를 비롯해 다양한 요인에 의해 변합니다. 따라서 알고리즘의 성능을 평가할 때는 최선과 최악, 평균의 시간 복잡도를 고려해야 합니다. 최선의 경우(Best-case)인 시간 복잡도는 알고리즘에 입력되는 데이터가 이상적일 때, 최악의 경우(Worst-case)인 시간 복잡도는 말 그대로 가능한 모든 시나리오 중 가장 최악(알고리즘의 실행 시간이 급격하게 커지는/느려지는 경우)일 때, 평균의 경우(Average-case)인 시간 복잡도는 알고리즘이 평균적으로 얼마나 빨리 실행되는지를 나타냅니다.
예를 들어 리스트의 요소를 하나씩 탐색한다고 할 때, 정말 운이 좋다면 탐색을 시작하자마자 첫 번째 항목에서 원하는 요소를 찾을 수도 있습니다. 이것이 바로 최선의 경우에 해당하는 시간 복잡도입니다. 반면에 찾으려는 요소가 리스트에 없다면 리스트 전체를 탐색해야 하는 최악의 경우에 해당하는 시간 복잡도인 것이겠죠.
리스트에 대한 순차 탐색을 100차례 수행한다고 하면 평균적으로 O(n/2)의 시간 안에 탐색이 끝날겁니다. 여기에서 O(n/2)은 빅 O 표기법을 통해 O(n)으로 표기할 수 있습니다. 일반적으로 알고리즘을 비교할 때는 평균의 경우인 시간 복잡도부터 살펴봅니다. 만약 더 깊이 분석하고 싶다면 최선과 최악의 경우인 시간 복잡도를 비교해 볼 수 있습니다.
✅공간 복잡도
알고리즘의 효율을 생각할 때는 컴퓨터의 메모리도 유한한 자원이므로 시간 복잡도뿐만 아니라 자원을 얼마나 사용하는지도 고려해야 합니다. 공간 복잡도(Space Complexity)는 알고리즘의 실행을 완료할 때까지 필요한 자원의 양, 즉 고정 공간, 데이터 구조 공간, 임시 공간의 메모리를 얼마나 사용하는지 나타냅니다. 고정 공간(Fixed Space)은 프로그램 자체가 차지하는 메모리를 말하며, 자료구조 공간(Data Structure Space)은 데이터 세트, 예를 들어 탐색의 대상이 되는 리스트를 저장하는 데 필요한 메모리를 말합니다. 알고리즘에서 이 데이터를 저장하기 위해 사용하는 메모리는 n의 크기에 따라 달라집니다.
또한 임시 공간(Temporary Space)은 알고리즘에서 중간 처리를 위해 사용하는 메모리, 예를 들어 데이터 전송을 위해 임시로 리스트 사본을 만들 때 필요한 메모리를 말합니다.
앞서 살펴본 시간 복잡도의 개념을 공간 복잡도에도 적용할 수 있습니다. n의 팩토리얼(factorial)(n 이하의 양의 정수를 모두 곱한 값)을 계산하는 알고리즘은 상수 공간 복잡도인 O(1)을 따릅니다.

이 알고리즘의 공간 복잡도가 상수인 이유는 n이 커져도 알고리즘에서 추가로 메모리를 사용하지 않기 때문입니다. 반면에 n까지 도달하면서 계산한 중간 결과를 모두 리스트에 저장한다면 이 알고리즘은 선형 공간 복잡도 O(n)을 따릅니다.

알고리즘에 필요한 공간 역시 n이 커지는 것과 같은 비율로 커지므로 이 알고리즘의 공간 복잡도가 O(n)이 됩니다. 시간 복잡도와 마찬가지로 알고리즘의 공간 복잡도 역시 상황에 따라 달라지지만 일반적으로는 공간을 적게 쓸수록 좋습니다.
✅복잡도가 중요한 이유
컴퓨터 과학자가 알고리즘을 최적화하기 위해서는 먼저 규모에 대해 이해해야 합니다. 알고리즘을 개선하고 싶다면 규모를 줄일 방안을 모색해야 합니다. 예를 들어, for 루프가 두 번 중첩된 O(n**2) 알고리즘이 있다고 합시다. 이 알고리즘을 최적화하기 위해 루프의 내부를 검토하는 것은 생각보다 중요하지 않습니다. 중첩된 for 루프를 사용하지 않을 수 있는지, 다시 말해 알고리즘의 규모를 줄일 수 있는지 판단하는 일이 훨씬 더 중요합니다.
같은 문제를 중첩되지 않은 두 개의 for 루프를 쓰는 알고리즘으로 풀 수 있다면 이 알고리즘의 시간 복잡도는 O(n)이 되고, 두 경우의 성능은 크게 차이나게 됩니다. O(n**2)인 알고리즘을 조정하여 아무리 효율을 올린다고 해도 O(n)으로 고쳐 쓰는 것에는 비교할 수 없습니다. 하지만 알고리즘의 최선 또는 최악의 경우를 고려하는 것도 중요합니다. 피치 못하게 O(n**2)인 알고리즘을 사용한다고 하더라도 최선의 경우에는 O(n)과 같은 결과를 낼 수 있고, 최선의 경우에 해당하는 데이터일 수 있습니다. 만약 이런 경우라면 O(n**2)인 알고리즘도 좋은 선택일 수 있습니다.
알고리즘을 잘 선택하는 것은 실제로 큰 영향을 미칩니다. 예를 들어 여러분이 웹 개발자이고, 사용자의 요청에 따라 알고리즘을 작성할 책임이 있다고 합시다. 상수 시간 알고리즘을 선택하는지, 2차 시간 알고리즘을 선택하는지에 따라 본인의 실력에 대한 평가가 엇갈릴 수 있습니다. 상수 시간 알고리즘을 선택해 1초 안에 고객의 요청을 처리할 수 있다면 고객은 다시 찾아오게 되고, 반대로 2차 시간 알고리즘을 선택해 고객의 요청을 1분 이상 지연시켰다면 그 고객은 두 번 다시 방문하지 않겠죠?
위 콘텐츠는 『이것이 자료구조+알고리즘이다 with C언어』와
『나의 첫 알고리즘+자료구조 with 파이썬』의 내용을 바탕으로 작성되었습니다.

이전 글 : [알고리즘 + 자료구조 = 프로그램] 자료구조의 개념과 종류
다음 글 : 모두를 놀라게 할 꼬마 링크의 새로운 등장
최신 콘텐츠
![[알고리즘 + 자료구조 = 프로그램] 최선의 알고리즘을 찾는 기준](/data/cms/CMS4190304964_thumb.png)
![[알고리즘 + 자료구조 = 프로그램] 자료구조의 개념과 종류](/data/cms/CMS2832062046_thumb.png)
