IT/모바일
[챗GPT] 그림으로 배우는 인공 신경망의 원리: 경사 하강법, 피드 포워드 신경망, 순환 신경망
챗GPT는 방대한 데이터로부터 패턴을 학습한 덕분에 전문가 수준의 정보부터 논리적인 답변까지, 사용자의 요구에 맞춰 묻는 말에 답할 수 있죠. 인공지능을 앉혀 두고 가르친 것도 아닌데, 어떻게 이런 일이 가능한 걸까요? 인공지능을 만드는 데 사용하는 인공 신경망의 작동 원리를 살짝 알아보겠습니다.
✅인공 신경망이란?
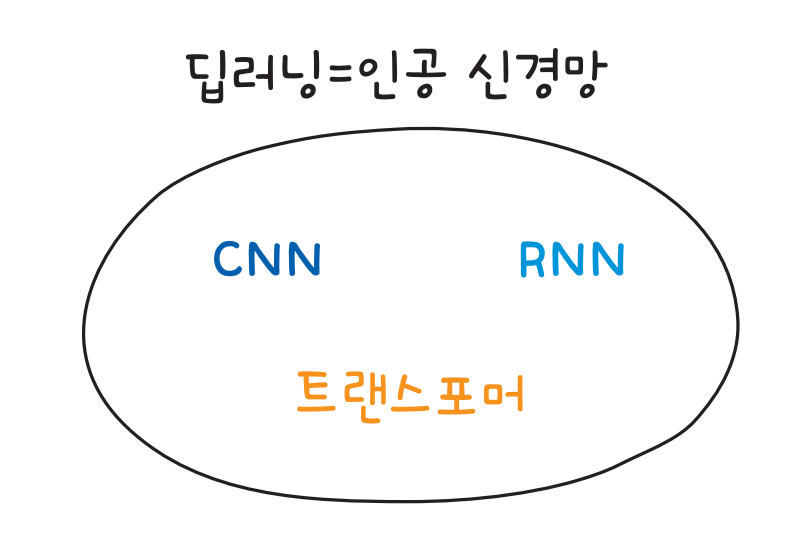
딥러닝은 인공 신경망Artificial Neural Network이라는 알고리즘을 대표하는 용어입니다. 딥러닝과 인공 신경망을 같은 의미로 생각해도 무방합니다. 인공 신경망의 구조는 단순하지만, 이를 레고 쌓듯 여러 겹 쌓으면 복잡한 모델로 확장할 수 있습니다. 이것이 인공 신경망이 가진 강력한 능력 중 하나죠.
머신러닝이 특정 알고리즘을 의미하는 것이 아닌 것처럼, 딥러닝도 특정 알고리즘을 콕 집어 지칭하지 않습니다. 예를 들면 피드 포워드 신경망Feed forward Neural Network, FNN, 합성곱 신경망Convolution Neural Network, CNN, 순환 신경망Recurrent Neural Network, RNN 등이 모두 딥러닝에 해당합니다.
한편, 신경망Neural Network이라는 이름이 붙지 않는 것도 있습니다. 오토인코더autoencoder, 생성적 적대 신경망Generative Adversarial Network, GAN, 트랜스포머transformer가 이에 속합니다.
그럼 인공 신경망, 즉 딥러닝은 어떻게 작동하는 걸까요? 어떻게 그렇게 뛰어난 성능을 낼 수 있는지 간단한 곱셈 접시라는 게임으로 가상의 인공지능이 어떻게 답을 맞히는지 살펴볼게요.
✔️인공지능과 곱셈 접시 게임하기: 경사 하강법
인공지능에게 딥러닝 알고리즘을 학습시킬 때, 경사 하강법이라는 방법을 씁니다. 경사 하강법이 무엇인지, 인공지능과 곱셈 접시 게임을 하며 알아보겠습니다. 알고 나면 너무 쉬운 개념입니다.
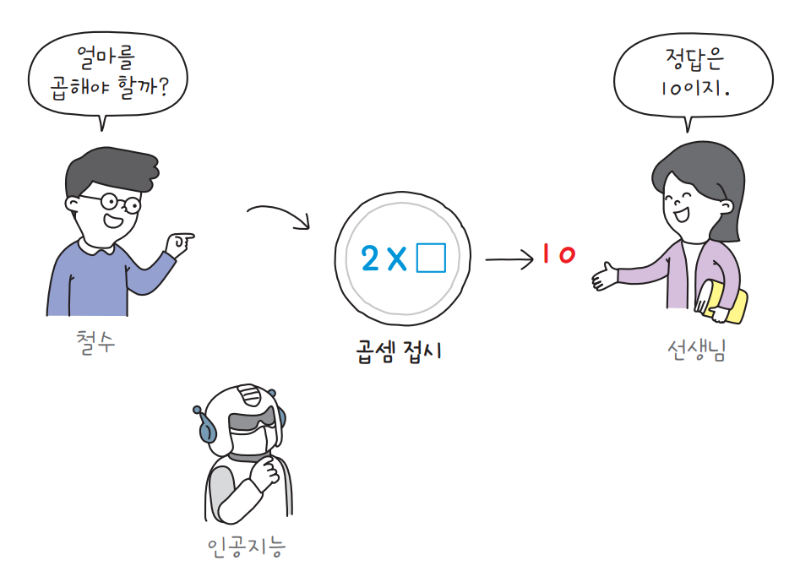
곱셈 접시 게임은 접시에 적힌 곱셈 식의 빈칸에 들어갈 숫자를 알아맞히는 게임입니다. 접시에는 ×라는 곱셈 식이 적혀 있습니다. 예를 들어, 철수가 첫 번째 빈칸에 2를 적고, 선생님이 곱셈의 결과로 10을 제시하면, 이제 인공지능은 2×=10에서 빈칸에 들어갈 숫자를 알아내야 합니다. 간단한 일차 방정식이죠.
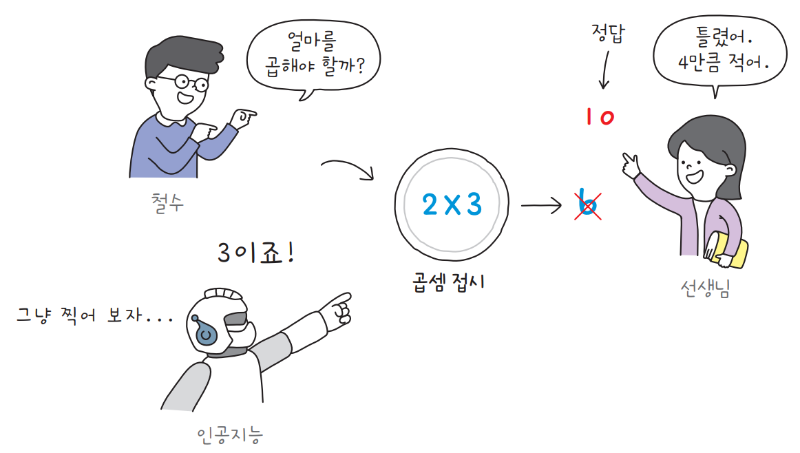
인공지능은 곱셈의 규칙을 몰라서 아무 숫자나 찍습니다. 인공지능이 빈칸에 들어갈 숫자로 3을 제시합니다. 선생님이 제시한 곱셈 식의 결과는 10이었죠. 인공지능이 빈칸에 3을 제시하면, 결괏값은 6이 되어 정답인 10보다 4만큼 작습니다. 이 차이를 선생님이 인공지능에게 알려 줘야 합니다.
인공지능에게 다시 기회를 주면, 아마 3보다 더 큰 값을 제시할 겁니다. 여전히 ‘얼마나’ 큰 값을 제시해야 하는지는 알지 못해서 정확한 값을 바로 제시하지 못합니다. 저런, 이번에도 틀렸습니다.
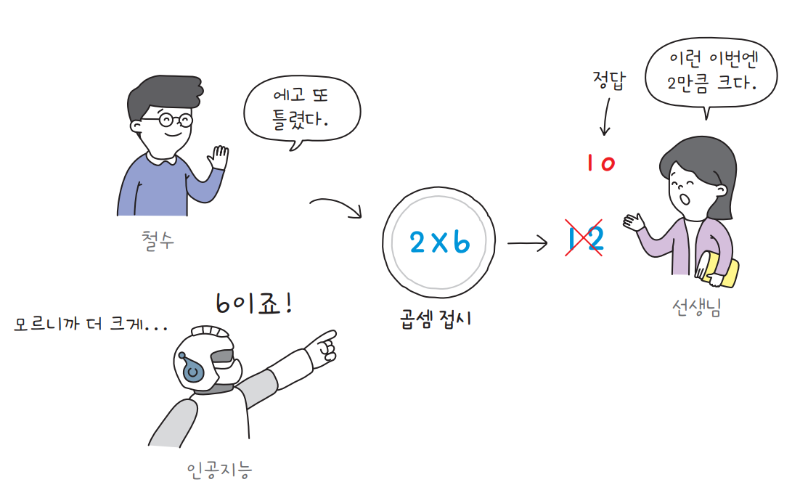
하지만 인공지능은 중요한 사실을 눈치챕니다. 빈칸에 3을 제시하면 결괏값이 4만큼 적고, 6을 제시하면 2만큼 많습니다. 오차가 점점 줄어들고 있죠. 그래서 다음에는 6보다 약간 더 작은 값인 5를 제시합니다. 드디어 정답을 맞혔습니다.
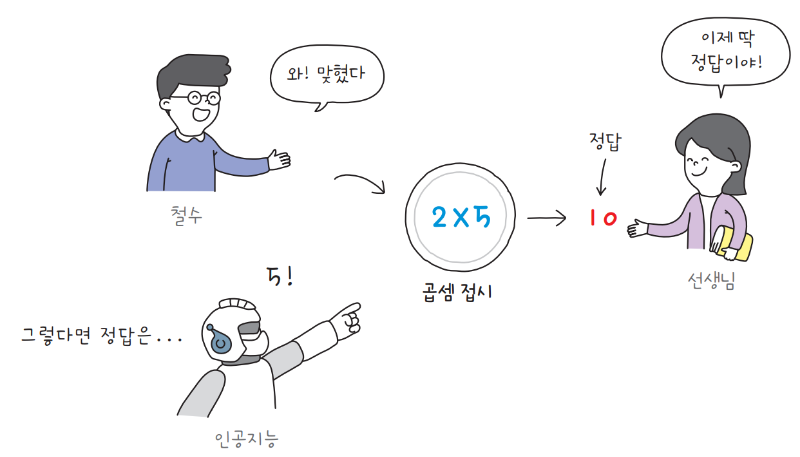
이렇게 정답에 가까운 값을 점진적으로 찾아가는 기법을 경사 하강법gradient descent이라고 부릅니다. 인공지능은 곱셈 접시 게임을 많이 할수록 능숙해집니다. 인공지능의 기초적인 알고리즘인 경사 하강법은 이게 전부입니다. 생각보다 쉽죠? 이런 곱셈 접시가 아주 많이 쌓이면 놀라운 일을 해낼 수 있습니다.
✔️더 많은 곱셈 접시 사용하기: 피드 포워드 신경망
경사 하강법은 분명 유용하지만, 현실 세계의 문제는 곱셈 접시 게임보다 훨씬 복잡합니다. 그래서 이번에는 곱셈 접시 여러 개를 나란히 배치해서 더 어려운 문제를 해결해 보려 합니다.
이제 곱셈 접시는 세 개입니다. 인공 신경망에서는 이런 곱셈 접시를 뉴런neuron 또는 유닛unit이라고 부릅니다. 그리고 곱셈 접시에 들어갈 정답을 모델 파라미터model parameter라고 합니다.
즉, 인공지능은 철수가 제시한 각각의 숫자에 모델 파라미터를 곱하고 그 연산 결과를 선생님이 제시한 정답과 비교합니다. 방식은 경사 하강법과 동일합니다. 처음에는 무작위로 아무 값이나 찍고, 점차 최적의 값에 가깝게 오차를 줄여 가며 정답을 찾습니다. 이러한 구조의 신경망을 피드 포워드 신경망이라고 합니다.
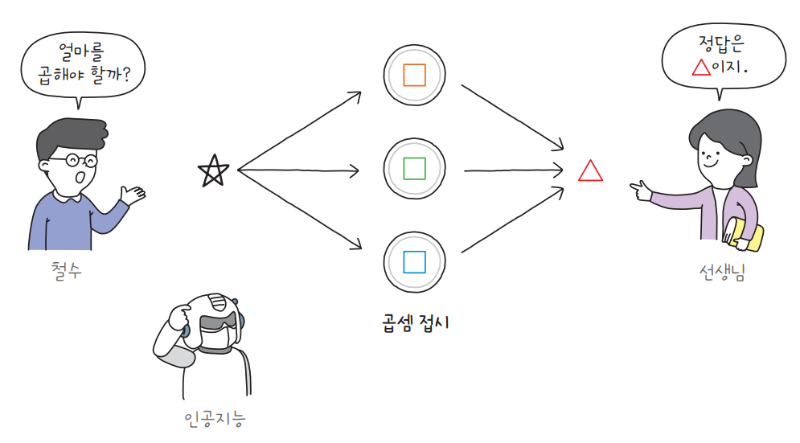
여기에서 중요한 것은 곱셈 접시가 가지고 있는 모델 파라미터가 모두 다르다는 것입니다. 모델 파라미터가 모두 동일하다면 입력에 곱할 규칙을 하나만 찾는 셈입니다. 하지만 곱셈 접시마다 모델 파라미터가 다르면 신경망이 다양한 규칙을 배울 수 있습니다.
문제가 더 복잡해지면 이런 곱셈 접시가 수십, 수백 개 필요할 수도 있습니다. 연구자들은 이런 경우에 곱셈 접시를 나란히 놓기보다는 여러 층으로 쌓는 것이 더 낫다는 것을 발견했습니다. 이를 그림으로 나타내면 다음과 같습니다.
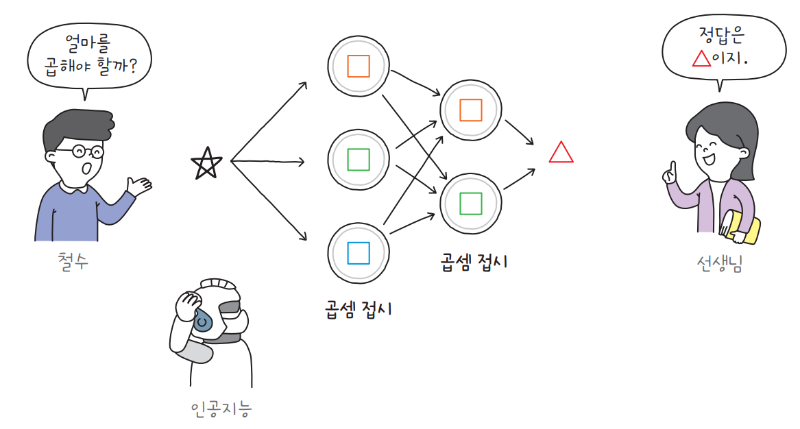
먼저 첫 번째 열에는 곱셈 접시를 세 개, 두 번째 열에는 곱셈 접시를 두 개 놓았습니다. 이렇게 한 열에 나열한 곱셈 접시를 인공 신경망에서는 층layer이라고 합니다.
여기에서는 곱셈 접시마다 하나의 모델 파라미터가 있지만, 일반적으로 인공 신경망에서 하나의 유닛은 여러 개의 모델 파라미터를 가집니다.
만,인공 신경망에 몇 개의 유닛을 놓아야 할지, 몇 개의 층을 놓아야 할지는 해결하려는 문제에 따라 다르지 일반적으로 유닛을 더 많이 배치할수록, 또 층을 더 깊게 쌓을수록 인공 신경망의 학습 능력은 증가합니다.
피드 포워드 신경망에서 정보는 한 방향으로만 이동합니다. 곱셈 접시 게임에 적용해 보자면, 철수가 제시한 숫자는 첫 번째 층의 모델 파라미터를 거쳐 두 번째 층으로 이동하는 것이죠. 피드 포워드 신경망은 구조를 이해하기 쉽기 때문에 많은 분야에서 응용되지만, 이전에 입력된 값을 기억하지 못한다는 단점이 있습니다.
예를 들어 인공지능에게 연달아 곱셈 접시 게임 세 문제를 제시한다고 가정해 보겠습니다. 다시 말해, 이번에는 철수가 세 개의 숫자 2, 4, 6을 연속으로 제시합니다.
우리는 철수가 2의 배수를 차례로 제시했다는 것을 금방 눈치챌 수 있습니다. 하지만 피드 포워드 신경망은 철수가 제시한 숫자 2, 4, 6 사이의 관계를 파악하지 못합니다. 반대로 6, 4, 2 순으로 숫자를 제시한다고 해도, 피드 포워드 신경망은 이를 전혀 알아차리지 못합니다. 즉, 피드 포워드 신경망은 순서가 중요한 데이터를 다루기엔 적절하지 않습니다.
우리가 사용하는 언어는 문자의 순서를 바꾸면 의미가 달라지기도 합니다. 따라서 신경망이 언어를 처리하려면 입력된 데이터의 순서를 고려해야 합니다. 그럼 어떻게 해야 할까요?
✔️곱셈 접시 순환시키기: 순환 신경망
순서에 의미가 있는 데이터를 처리하기 위해 순환 신경망이 고안되었습니다. 순환 신경망의 구조를 직관적으로 설명하기 위해 여러 개의 곱셈 접시가 담긴 큰 쟁반을 상상해 보겠습니다.
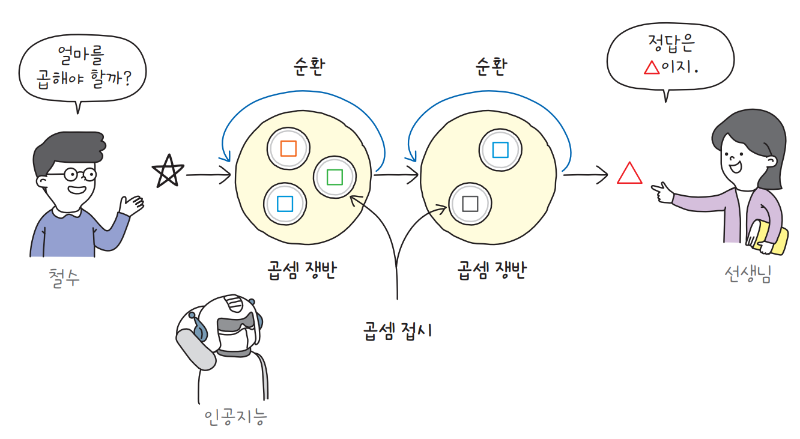
곱셈 쟁반에는 여러 개의 곱셈 접시가 담겨 있습니다. 이 쟁반을 순환 신경망에서는 셀cell이라고 부릅니다. 여러 개의 유닛을 한 데 모으면 셀이 되는 것이죠.
첫 번째 곱셈 쟁반이 출력한 값은 다음 번 계산에 입력으로 재사용됩니다. 즉, 출력이 순환되어 자기 자신에게 다시 전달됩니다.
이런 구조적인 특성 덕분에 순환 신경망은 순서가 있는 데이터, 즉 언어나 시계열 데이터time series에서 뛰어난 성능을 보입니다. 이전에 처리한 결과가 다음 계산에 재사용되므로 순서에 대한 패턴을 학습할 수 있는 것이죠.
지금까지 곱셈 접시를 사용하여 피드 포워드 신경망과 순환 신경망의 구조에 대해 알아보았습니다. 순환 신경망이 언어를 다루기에 적합한 모델이지만 요즘에는 거의 모든 언어 모델이 순환 신경망 대신 트랜스포머를 사용합니다. 트랜스포머는 무엇인지, 어떤 장점이 있는지 GPT에 담긴 기술이 궁금하다면 『인공지능 전문가가 알려 주는 챗GPT로 대화하는 기술』에서 확인해 보세요.
위 콘텐츠는 『인공지능 전문가가 알려 주는 챗GPT로 대화하는 기술』의 일부를 발췌하여 작성되었습니다.
최신 콘텐츠
